1
| |
i need help for my upcoming calculus final. a couple problems i dont get... i'd appreciate it if anyone can help...
the teacher gave the answers, but obviously i don't know how to show the work for it.

edit: for #4, the top x is supposed to be a dx.
answers here:
+ Show Spoiler +
1) x=110, y=220/pi
my thought process is area of a circle + area of the rectangle = 440? but i didn't know how to set it up
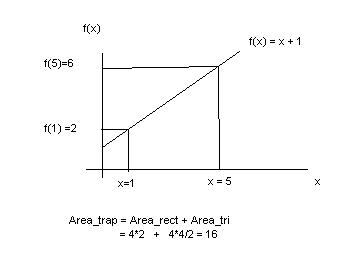
2) answer = 16.
i can do this problem through sum of the area of rectangles (area under the curve) and by the fundamental theorem of calculus, but i dunno what it means by using trapezoids)
3) answer = sin^3x/3 + c.
i tried deriving the answer and all i get is sin^2x. i don't know what happens to the cosx? or maybe i just suck at math (yes)
4) answer = ln4. again, totally lost and simply don't know how to set it up.
|
|
| | Last edit: 13/12/2009 20:43 |
|
|
1
 |
SugoGosu Korea (South). Dec 13 2009 20:41. Posts 1793 | | |
rofl i forgot all of calc. last semester after it finished. shit.... |
|
| Say this outloud! Why was six afraid of seven?......Because Seven Eight Nine | |
|
|
1
 |
genjix China. Dec 13 2009 20:46. Posts 2677 | | |
1. find a formula for the area of that box + circles.
then differentiate and find the maxima- thats where dy/dx = 0
2. (5+1)*(1+1)*(5-1)/2 (area of a trapezoid)
3. look it up the formulas and whatnot
4. split that fraction into 2 parts... integ(1/x) = lnx |
|
| If you wish to make an apple pie from scratch, you must first invent the universe. | |
|
|
1
| |
for number 2, you're saying 6*2*4/2? the answer is 16 though. |
|
|
1
 |
nixxxbg Bulgaria. Dec 13 2009 21:12. Posts 436 | | |
Here's prob 2
|
|
|
1
 |
domyouji Zimbabwe. Dec 13 2009 21:17. Posts 435 | | |
for some reason that field looks like a weiner |
|
| to live the dream you gotta play the game | |
|
|
1
 |
Jonoman92 United States. Dec 13 2009 21:17. Posts 280 | | |
For problem one I think I can tell you how to start:
It's an optimization problem:
-first off 2x + 2(pi)(y/2)=440 (that is the total perimeter and is your constraint) (This is the straight sides (2x) plus the semicircle curves, (y/2) is the radius, 2(pi)(r) is circumference)
-secondly the equation you want to optimize is just xy=Area
From here I think you need to use substitution to plug one equation into the other only using one variable (at least this is how I would do it, it's not the only way.) ie: -(2(pi)(y/2) - 440)/2=x
Dunno if what I just said is actually right. |
|
| ~~sMi.Arcology SC For Life! | |
|
|
1
 |
nixxxbg Bulgaria. Dec 13 2009 21:23. Posts 436 | | |
Prob 3:
Let u = sin(x); du = cos(x)dx
Then: INT u^2 du = u^3/3 + const = (sin(x)^3)/3 + const |
|
|
1
 |
nixxxbg Bulgaria. Dec 13 2009 21:27. Posts 436 | | |
Prob 4:
d/dx (log(1-x)) = -1 / (1-x)
Then:
INT 1/(1-x) dx = -log(1-x) between 0 and 3/4 = -(log(1-3/4) - log(1)) = -log(1/4) = -(log(1) - log(4)) = log(4)
**Note1: if you dont see this, let u = 1-x, du = -dx
**Note2: log(1) = 0 |
|
|
1
 |
Patrocle France. Dec 16 2009 13:31. Posts 623 | | |
PM me if you are still lost.
|
|
| An apple a day keeps the doctor away | |
|
|
1
| |
Your mistake in the answer for problem 3 is that u forget the inner derivative of sinx that is exactly cosx.
DER( (sinx)^3/3) = (sinx)^2 * cosx |
|
|
1
| |
| | On December 13 2009 20:17 Jonoman92 wrote:
For problem one I think I can tell you how to start:
It's an optimization problem:
-first off 2x + 2(pi)(y/2)=440 (that is the total perimeter and is your constraint) (This is the straight sides (2x) plus the semicircle curves, (y/2) is the radius, 2(pi)(r) is circumference)
-secondly the equation you want to optimize is just xy=Area
From here I think you need to use substitution to plug one equation into the other only using one variable (at least this is how I would do it, it's not the only way.) ie: -(2(pi)(y/2) - 440)/2=x
Dunno if what I just said is actually right. |
Think that's right. After that
y*x = -y*(2(pi)(y/2) - 440)/2 = (440y - pi*y^2)/2
which is the function to maximize, and how do we maximize a negative second degree, yeah we derive it and set it to zero and there's our answer.. |
|
|
|

 Contact Users: 736 Active, 0 Logged in - Time: 09:44
Contact Users: 736 Active, 0 Logged in - Time: 09:44